Two days experimenting with a sensor, three for gathering parts, soldering and thinking about implementation details. Tuner determines string sound frequency by illuminating it with infra-red light emitting diode and gathering string "blinks" with an optotransistor.
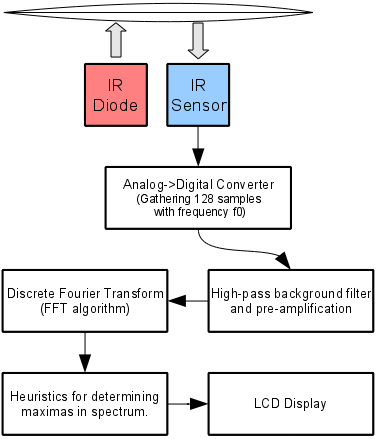
Sensor required to gather information about string vibrations is built using two parts (4 including resistors):
- Light emitting diode - infra-red diode which is simply shining upon the string. Nothing fancy, i.e. no blinking with special frequency. This diode of course requires resistor, about 300 ohms. It's good to start with potentiometer so one can adjust led brightness.
- Optotransistor - (in short it's an element with a resistance which varies according to amount of light received). It's connected between any ADC pin of AVR and the ground. ADC pin should also have 10k pull-up. The more it's illuminated the lower voltage is visible by ADC.
The same design can be used in collision-evasion sensors I guess...
For reference here are the frequencies of all string in standard E-tuning: e 329.628, H 246.942, G 195.998, D 146.832, A 110.000, E 82.407.
Say we want to tune the string E. I want to gather 128 samples and then calculate their spectrum using Discrete Fourier Transform. It's important to set correct sampling frequency so the frequency we're tuning is clearly visible in the spectrum, while other (possibly irrelevant) frequencies are filtered out - I decided on locating it exactly in the middle.
Now. There's Nyquist theorem saying that the with the sampling frequency f_0,
the highest frequency I can "observe" is f_0 / 2. Right? Therefore the resulting
spectrum for 128 input samples consists of only 64 "bars". Each bar refers to
some frequency. Value of each bar tells us how big is the amplitude of a sinus
component of this frequency.
Now for a bit of math. To better see what I'm talking about see a spectrum gathered from AVR with serial port (click for bigger):
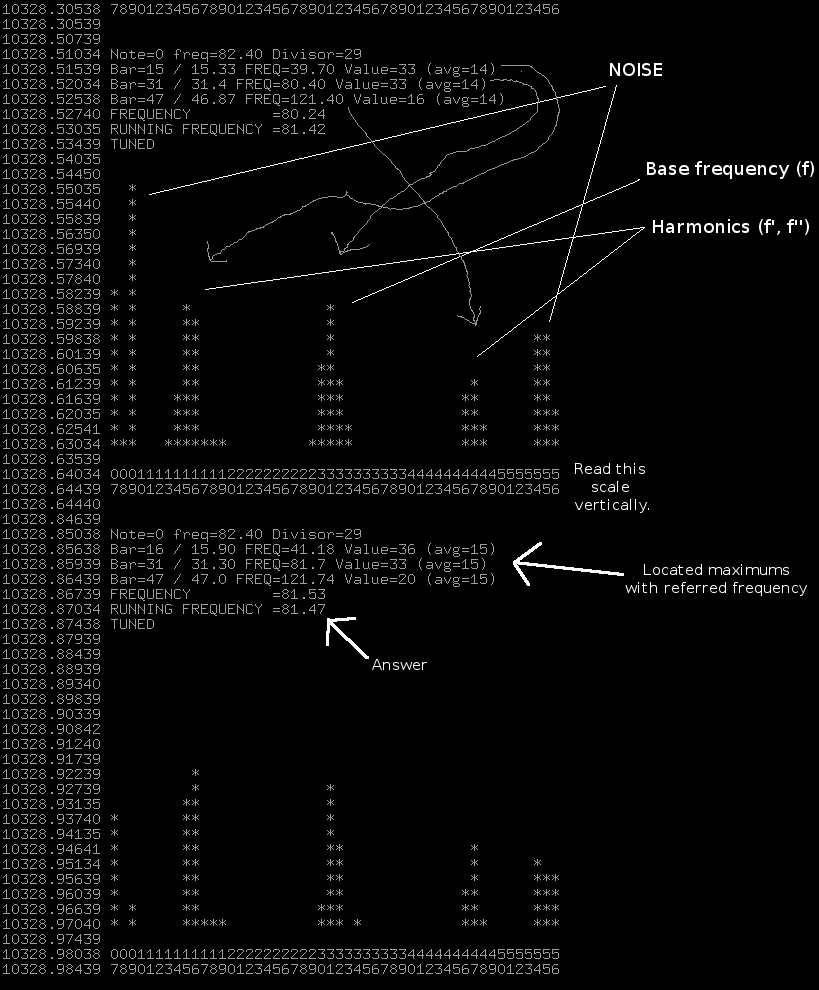
64th bar refers to highest frequency (f_0/2), and therefore middle bar (32th)
will refer to half that frequency - f_0/4. We want f_0/4 to be equal to 82.4Hz.
16*10^6 - my quartz frequency. 13 - cycles required for ADC conversion. 128 - my
ADC clock prescaler. D - divider, number of ADC conversions I simply DROP to get
correct sampling frequency. 16*10^6 / 128 / 13 / D / 2 = f_0. Okay?
So frequency 'f' of 'B' bar (counting from 1) is 16\*10^6 / 128 / 13 / D / 2 *
(B/64) = f. (I use Maxima) Let's see solution forB = 32, f = 82.407:
(%i4) solve(16*10^6 / 128 / 13 / D / 2 * (B/64) = f, D), f = 82.407, B=32, numer;
(%o4) [D = 29.17041198501873]
Okay. Whole algorithm looks like this:
1. Set up ADC so sampling frequency is OK. For E string I used /128 prescaler
and used one measurement in 29. Additionally I estimate sensor "background"
using simple low-pass filter and subtract it from measurements.
2. Calculate FFT of the sample. I didn't have to write my own, as there's great
FFT for AVR.
3. Using some heuristics I locate all 'peaks' in spectrum (which are supposed to
show base frequency of signal (f) and at least two of it's harmonics f'=f/2
and f''= f*3/2). Choose some of them, and calculate signal frequency using
their waged average. f_out = (f + f'*2 + f''*2/3) / 3. I use three harmonics
to increase accuracy... generally only one should be enough. I also locate
'peaks' in spectrum with "sub-bar" approach... that is: I locate peak,
average it's neighbourhood and therefore I can say that it's located at 32.45
(between 32 and 33 bar) instead of just saying that it's 32 bar. That is kind
of important because using only 64 bars, bar 32 refers to 82.89Hz and 33 to
85.48Hz frequency. This point in algorithm can certainly be improved.
4. And finally I display the result.
My design involves ATmega (must have MUL instruction available) with enough RAM for FFT buffers. I used ATmega32 with 2k, but by using some tricks with union I need only a bit more than 1k. Also my final design has a 2x8 character LCD. Substituting it with simpler LEDs should allow to fit whole code in less than 1k. That would allow use of the ATmega8 which is significantly smaller. I used 16Mhz clock, which also requires >= 4.5V voltage. I believe this is perfectly doable with 8Mhz, so one should be able to use 3V battery without any stabilization.
Here you have the code: Light Guitar Tuner 0.1 and if you like, a GPG signature.
For early tests it's fine to use... lamps in your house. In Europe we've got 50Hz in power lines, which makes lights blink with 100Hz harmonic which is perfectly visible in FFT spectrum. Using this as a reference I could say that my tuner has 1Hz accuracy for 110Hz frequency (string A). [Note from 2018: currently LEDs might not blink that visibly].
Should you use it - please tell me how does it work for you.
Comments