The need

I was analyzing a network traffic to devise a way to detect a link bandwidth saturation without introducing a lag. That is: terabits of traffic pass through routers. Routers sample the traffic (1:100 packets or 1:1000) and generate meta information about observed "flows" of data (Netflow).

I aggregated all the flows by physical links they will be going through, and at some point I ended up with a timeseries signal - a series of noisy measurements and a classical problem: apply a real-time low-pass filter to the data.

In a nutshell:

Real traffic -> Router [Statistical sampling -> Flow caching] ->
-> Netflow -> 
Detector [Traffic aggregation per link -> Filtering -> Overflow/anomaly detection]

The problem

Network traffic doesn't behave like water in tubes - it's not physical. It's discreet (split into packets ranging usually from ~64 to 1500 bytes), it's bursty (periods of high traffic followed by silence), and the observed metadata behaves differently depending on the type of the traffic (smooth TCP flows vs single UDP packets with spoofed src IPs) increasing the problem.

The higher the bandwidth though, the more stable it gets. To reach a 5-40Gbit/s ranges you usually have to transmit from multiple - not perfectly synchronized - sources. The traffic requires then a bit of a time to fade in and fade out - behaves like an "Ohh" going through the crowd during the keynote at an IT conference.

The obvious solution

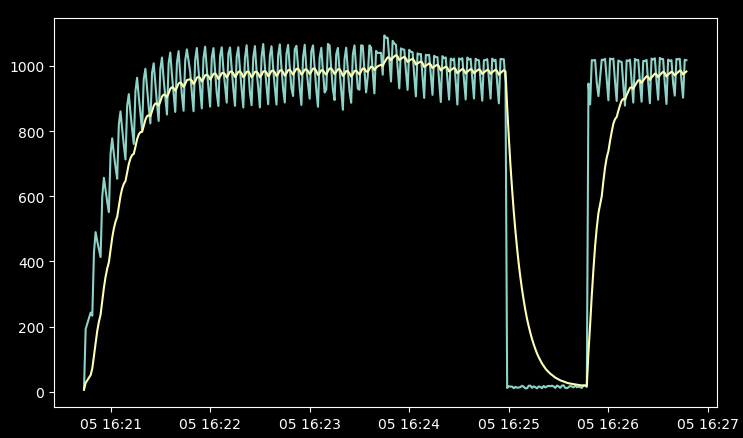
Initially I implemented a "weighted moving average", which worked, but required a high weight to get rid of oscillations. High weight introduces a delay in a filtered signal, which will increase a detection lag - something I explicitly tried to avoid.

Implementation is quite simple though and can be easily optimized in Python using numpy. Every second, for each new value following operation executes:

filter_output = WEIGHT * previous_output + new_unfiltered_measurement
filter_output = filter_output / (WEIGHT + 1)

Note: this can be be altered to use a smaller weight for new_signal>filtered case, and bigger for the new_signal<filtered case. This might be useful for speeding up detection of overflows.

Input signal (greener) and moving average response for a multi-source UDP traffic of around 100Mbps and 1Gbps:

The professional solution

Next, I tried implementing the Kalman filter. I've used it before for filtering physical measurements using multiple sensors and when done properly it always performs outstandingly. The complexity of the solution grew though and I had a problem with designing a good state matrix - after all the network traffic is not really a kinetic problem.

Kalman, in simplest case, works just like the moving average filter, but the weight (called Kalman "gain") is automatically calculated by observing the measurement noise and differences between predicted state and current state.

Kalman filter implementation would certainly be doable and probably not that complicated, but since I was already out of time to do the research, I decided to drop this idea.

Not-so-obvious solution

Eventually it occurred to me that maybe this "statistical meta information on the network traffic" doesn't represent a physical process, but I'd certainly like it to - be less random, less oscillating and a bit more persistent.

We can think about the filter output as a position of a heavy ball. The filter input tells it where the ball have to go eventually, but it can't just teleport, it needs to gain momentum. That's how the filtering problem becomes a problem of applying control. And for controlling we have a known and liked (and hated) solution - the PID controller.

The ball has position and speed. Each time the new measurement comes the speed is altered by the PID and position is altered by the ball speed. PID output therefore applies a force or acceleration to the ball.

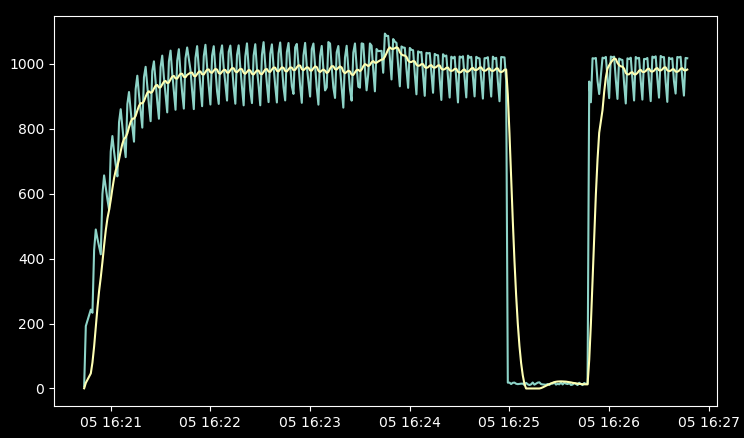
Input signal and PID filter response - notice time to settle in comparison to a moving average.

The summary

PID is mathematically simple, easy to implement with numpy for multiple values but requires calibration. P component alters the speed proportionally to the difference of the ball position and the measurement. Setting high P coefficient makes the PID respond faster to changes than the moving average did. D component dampens oscillations and I component pushes the ball toward correct position when the proportional component becomes to small to do it fast enough. Calibrating for different traffic types took me around 15 minutes.

I decided to publish a note, because I haven't found much on using PID controller as a filter and it wasn't obvious to me at first. This approach was most probably used before, but any similar articles are probably hidden behind layers of articles on filtering inputs or outputs of a normal PID controllers which make it harder to duck(duckgo) them up.

Sensible interpretation of a netflow information, for a traffic ranging from 100Mbps to 10Gbps, without incurring additional lag is a different problem and a different algorithm. Probably interesting topic on its own.